¿Son difíciles las matemáticas? Obviamente sí

Tuve la idea de escribir este artículo, a raíz de una conversación (muy agradable como todas las que mantengo con personas de GEOSEN), con unos amigos, colegas y experimentados geólogos de la citada asociación. Ahora bien en este caso el asunto de debate no era la geología. Eran las matemáticas. Resulta que hacía algunos días, yo había dicho que para estudiar matemáticas, lo único necesario es pensar. Como pensar es algo que todos podemos hacer, la conclusión que podría deducirse es que las matemáticas son una rama del conocimiento sencillísima, quizá la más sencilla, vamos la más fácil de aprobar de todas las asignaturas. Esto es una conclusión totalmente equivocada. A veces las prisas por hablar antes de pensar un poco, nos llevan a cometer estos despistes. Eso me pasó.

Otra cuestión (y esto voy) es que las matemáticas, se puedan aprender en muchos  aspectos de las mismas, simplemente pensando a diferencia de lo que sucede en otras áreas del conocimiento como la historia, la geografía o los idiomas. Hace algún tiempo (junio de 2023) escribí en este mismo medio un artículo titulado: “Las matemáticas parecen…¡la cara de Dios!” en el que ya hablé de este asunto. Se localiza este artículo en la Red. Ahora insisto en que en el campo de las matemáticas, es esencial pensar y para justificar esta afirmación voy a poner varios ejemplos fáciles de entender.

La práctica (nos la enseñaron cuando éramos muy niños en la escuela del pueblo) de dejar un espacio, (uno y sólo uno) a la derecha en aquellas cuentas de multiplicar dos cantidades de varias cifras, nunca me la explicaron a mi. Me decía el maestro (y los libros) que había que hacerlo así y punto. Ahora ya camino de los 70 “añazos”, me puse un día a ver porqué ha de ser así. Es fácil entenderlo. Puede comprobarlo el lector por si mismo. Hay infinidad de ejemplos similares. Es obvio que para sumar o restar quebrados, hay que reducirlos previamente a común denominador. Pensemos que un cuarto más un tercio, son 7 doceavos y que un tercio menos un cuarto es sólo un doceavo. Creo que son asuntos tan sencillos que la mayoría de las personas entienden. Para multiplicar o dividir sin embargo, no es preciso hacer una reducción previa a denominador común. Es también sencillo de entenderlo… al margen de lo que diga o no el libro de texto.

Esto que sucede con las operaciones con quebrados (de la escuela del pueblo), sigue estando presente a otros niveles. Por ejemplo la geometría y trigonometría básicas. Es obvio que la suma de los tres ángulos de un triángulo ha de ser exactamente 180 grados sexagesimales y si se trata de un polígono de 4 lados justamente el doble. Así podríamos seguir con muchos casos más… las funciones matemáticas, las derivadas, las integrales y el cálculo matemático en general. En mi vida profesional a menudo tuve que dedicarme a la topografía, utilizando instrumentos bastante anticuados. Similares a los que se usaban en el siglo XIX e incluso antes. En tales circunstancias a veces tuve que medir distancias por métodos indirectos. En estos casos es esencial discurrir y pensar mucho al margen de conocimientos memorizados. Es algo comprobado desde hace siglos. Pensemos por ejemplo, en el conocidísimo problema de Pothenot cuya resolución se remonta a varios siglos atrás. Ahora bien esto no supone en modo alguno que en el campo de las matemáticas, además de pensar sea preciso también memorizar.  Esta es la cuestión, pensar mucho muchísimo y … ¡además memorizar!.

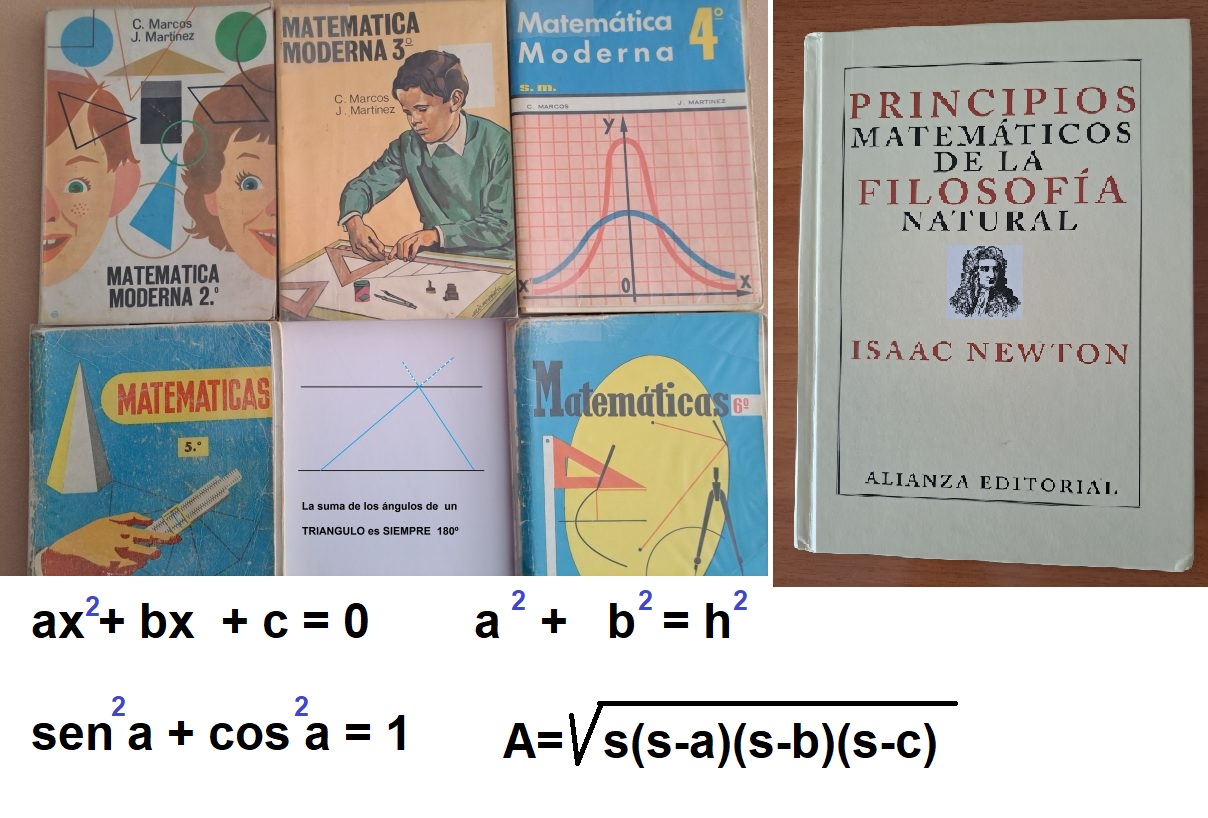
  DIFICULTAD PARA APRENDER MATEMATICAS

La necesidad  de memorizar para saber matemáticas se pone de manifiesto en el estudio de asuntos tan conocidos como el teorema de Pitágoras. Al parecer existe una amplísima gama de modos de demostrarlo…simplemente pensando. Yo así de entrada sólo conozco una. No obstante, aun cuando supiera decenas de ellas, esto no implicaría que no fuese preciso memorizar, pera no confundir los catetos con la hipotenusa. Si lo hacemos nos podrían llamar (y con razón), “catetos”.

Por lo que respecta a los conocimientos que es proceso memorizar en el ámbito de las matemáticas y empezando por lo más básico, hay que aprender los nombres de las diferentes operaciones matemáticas, los nombres de las partes de un quebrado, los nombres de las diferentes funciones trigonométricas…y así podríamos seguir más y más. La realidad es que en la asignatura de matemáticas hay que memorizar (como en muchas otras) y además pensar. Trabajo doble pues. Aquí está la clave. Por ello las matemáticas no pueden ser una asignatura más fácil que las demás, es justo al revés. A este respecto yo mismo he escrito en alguna ocasión, por ejemplo al hablar sobre la hidrogeología, que es una rama de las ciencias geológicas que busca agua subterránea de modo racional; que las matemáticas son tan difíciles que yo mismo soy incapaz de entender muchos de sus conceptos. Yo no soy capaz de entender, por ejemplo la ecuación de Laplace, que debería dominar desde que era estudiante universitario.

Añadiré algo más. Hace años en una revista que publica la Asociación Leonesa de Astronomía, alguien escribió según recuerdo que intentando leer la celebérrima obra de Newton (“Principios Matemáticos de la Filosofía Natural”) sólo era capaz de leer ¡una página por día!. En esa revista suelen escribir personas con elevados conocimientos matemáticos y por ello yo quise leer esa obra de Newton. Hace ya muchos años que tengo en casa el libro, pero…no soy capaz de leer y entender ni una sola de sus páginas, cuando figuran razonamientos matemáticos. Supongo eso si que una persona con gran capacidad intelectual (Newton por ejemplo), con un gran esfuerzo pueda ser capaz de descubrir por si misma toda la cantidad de leyes matemáticas, que se enseñan en los libros; pero la mayoría de los mortales necesitamos ayuda para descubrir las leyes matemáticas. Por ello  para aprender matemáticas, hay que pensar mucho y además memorizar también mucho.

Tengo entendido que en algunas ocasiones a la hora de resolver problemas de cálculo complicados (integrales triples por ejemplo), se les permite a los alumnos utilizar el libro o libros de texto, porque el profesor es consciente de que aún así es complicado resolver ciertos cálculos matemáticos. Esto no puede suceder en un examen de historia, geografía, lenguaje o literatura universal.

El origen de este tema estriba en la mala (malísima) opinión que yo tengo sobre el actual sistema de enseñanza hoy imperante en España. En mis tiempos de estudiante, me parece, las cosas no eran así. Pero este es un problema diferente y que además me parece que no tiene solución. Es un problema social más de los muchos que padecemos.

Madrid 4 de febrero de 2024//Rogelio Meléndez Tercero